Pascal: Вычисление интеграла методом Симпсона
Для того, что бы понять, как это работает нужно обратиться к геометрическому смыслу интеграла.
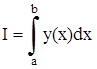
Интеграл численно равен площади криволинейной трапеции, ограниченной кривой y(x), прямыми x=a, x=b и отрезком [a; b] оси Ox.
Формула Симпсона:
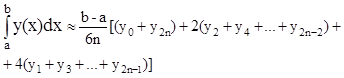
с геометрической точки зрения означает, что график функции y(x) заменен другой кривой j(x), состоящей из дуг парабол: каждая сдвоенная дуга кривой y(x) заменяется параболой. За приближенное значение интеграла I принимается площадь криволинейной трапеции, ограниченной кривой j(x), прямыми x=x0, x=x2n и отрезком [x0, x2n]. Таким образом, решение сводится к программированию алгоритма вычисления площади криволинейной трапеции.
Программа, которая вычисляет такой интеграл:
[pascal]
program Simpson;
uses crt;
var
x,a,b,h,s:real;
n:integer;
function Y(t:real):real;
begin
Y:=sqrt(1+t*t+t*t*t*t);
end;
begin
clrscr;
write(‘Отрезок интегрирования [a,b] ?’);
read(a,b);
write(‘На сколько частей нужно разделить отрезок? n=’);
read(n);
h:=(b-a)/n;
s:=0; x:=a+h;
while x<b do
begin
s:=s+4*Y(x);
x:=x+h;
s:=s+2*Y(x);
x:=x+h;
end;
s:=h/3*(s+Y(a)-Y(b));
writeln;
writeln(‘Интеграл = ‘,s);
readkey;
end.
[/pascal]
Программа запрашивает отрезок интегрирования. Сначала число снизу интеграла, потом сверху. После этого спрашивает, на сколько отрезков делить функцию? Таким образом, чем больше это число, тем выше точность вычислений.
Код на C# здесь
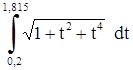
Найдена ошибка аргумента. Исправлено.
Слишком маленькими отрезки делать тоже не стоит. Я сделал отрезкок 1/1000000, вычисления дали большую погрешность; а при отрезке 1/100000 все было приемлемо.
Может у тебя округлило?
все понял кроме этой части
begin
s:=s+4*Y(x);
x:=x+h;
s:=s+2*Y(x);
x:=x+h;
end;
s:=h/3*(s+Y(a)-Y(b));
writeln;
можешь объяснить?
А это сам метод.
Спасибо за код.
Кстате в цикле можно еще так организовать чередование индексов 2 и 4:
взять любую переменную равную единице, например c:=1;
и в цикле считать сумму примерно так:
s:=s+(3+c)*f(x);
c:= -c;
тогда каждый раз в скобках (3+с) будет 2 либо 4.
Спасибо, все прекрасно работает, но не могу понять этой формулы в коде:
s:=h/3*(s+Y(a)-Y(b))
Ведь исходя из формулы Симпсона значения начала отрезка и его конца СКЛАДЫВАЮТСЯ, а в нашем случае между ними знак минус ?
С вами согласен!
C3:=h/3*(C3+y(a)+y(b));
должен быть плюс