C#: Простые числа методом перебора
Простые числа. Иногда появляется необходимость определить простое ли число или нет.
Если взять теорию, то простое число-это такое число, которое делится только на себя и на единицу.
Для того, что бы узнать, число является или не является простым, нужно либо перебрать все числа до этого числа, либо, по одной из теорем, достаточно перебрать все числа до корня из этого числа.
Реализовал вот такую функцию на C# :
[csharp]
static bool isPrime(int number)
{
if (number < 2) return false;
for (int i = 2; i <= Math.Sqrt(number); i++)
{
if (number % i == 0) return false;
}
return true;
}
[/csharp]
Функция булева типа, следовательно, возвращает true или false. А внутри всё так:
Первое условие нужно для того, что бы пресечь попытки передать недопустимое число. Простые числа можно считать только начиная с двойки. Далее цикл от 2х соответственно до корня из числа. Прошу обратить на не строгое условие в сравнении. В цикле я проверяю, делится ли число (остался ли остаток от деления его на i) на i и если хоть одно число, остаток которого стал равен нулю (число разделилось на что-то еще нацело) то выходим из функции со значением false.
блока else нет, так как зачем проверять это? Если не вышли в цикле, то число явно простое.
Использование:
Пример 1 (для последовательности)
Примечание: использование этой функции достаточно медленно, так как приходится перебирать все числа до искомого каждый раз.
[csharp]
static void Main(string[] args)
{
int input = int.Parse(Console.ReadLine());
for (int i = 2; i <= input; i++)
{
if (isPrime(i))
{
Console.WriteLine(«Число {0} простое», i.ToString());
}
else
{
Console.WriteLine(«Число {0} Непростое», i.ToString());
}
}
}
[/csharp]
Пример 2 (для одиночного числа)
[csharp]
static void Main(string[] args)
{
int input = int.Parse(Console.ReadLine());
if (isPrime(input))
Console.WriteLine(«Число {0} простое», input.ToString());
else
Console.WriteLine(«Число {0} Непростое», input.ToString());
}
[/csharp]
Есть еще метод решетки Эратосфена, но о нем чуть позже.
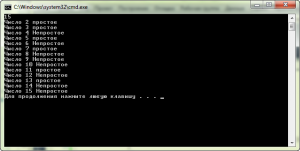
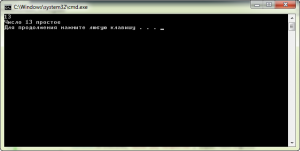
не работает, пишет что isPrime не существует в текущем контексте(
Программа отлично работает, просто вам нужно вставить функцию isPrime в код, а она описана выше