Недавно писал уже о нахождении простых чисел методом перебора. Метод конечно работает, но у него есть одна проблема — медленный он.Чуть более быстрый метод — это решето Эратосфена.
Описание алгоритма из Википедии:
Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
- Пусть переменная p изначально равна двум — первому простому числу.
- Считая от p шагами по p, зачеркнуть в списке все числа от 2p до n кратные p (то есть числа 2p, 3p, 4p, …)
- Найти первое не зачеркнутое число, большее чем p, и присвоить значению переменной p это число.
- Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n
Но псевдокод, который написан на странице при точном кодировании у меня не заработал. Может у меня руки кривые? :) Реализовал опираясь на C++ версию, написанную каким-то человеком на форуме.
[csharp]
static void Main(string[] args)
{
int n = int.Parse(Console.ReadLine());
bool[] A = new bool[n];
// Инициализация и вывод массива
for (int i = 2; i < n; i++)
{
A[i] = true;
Console.Write(«{0} «, i);
}
// Обработка
for (int i = 2; i < Math.Sqrt(n) + 1; ++i)
{
if (A[i])
{
for (int j = i * i; j < n; j += i)
{
A[j] = false;
}
}
}
Console.WriteLine();
// Повторный вывод
for (int i = 2; i < n; i++)
{
if (A[i])
Console.Write(«{0} «, i);
}
}
[/csharp]
Один момент тут интересный. Может возникнуть вопрос, нафига нужно использовать булевский тип? Просто потому, что нам не нужно знать значение (для этого у нас есть переменная i, которая хранит позицию), а нужно лишь знать простое оно или нет, true или false. Изначально имеем массив где все ячейки имеют значение true, а затем лишь меняем эти значения на false и в итоге получаем массив где в нужных позициях осталась истина.
И скрин работы приложения:
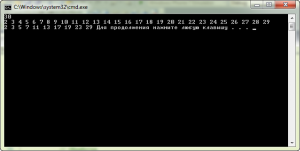
Если заполнить массив рандомом, то функция пропускает 4,6,9 и иже с ними
Если количество чисел будет само простым числом, то в ответе оно не будет написано. А это есмь недочёт. B>)